П. А. Флоренский

 

МНИМОСТИ В ГЕОМЕТРИИ

                                                РАСШИРЕНИЕ ОБЛАСТИ

                                                ДВУХМЕРНЫХ ОБРАЗОВ

                                                ГЕОМЕТРИИ

 

                                                ОПЫТ НОВОГО

                                                ИСТОЛКОВАНИЯ

                                                МНИМОСТЕЙ

 

 

 

 

 

                                               Издание второе

 

 

 

 

Флоренский Павел Александрович

Мнимости в геометрии: расширение области двухмерных образов геометрии

(опыт нового истолкования мнимостей). Изд. 2-е.

М.: Едиториал УРСС, 2004. — 72 с.

(Академия фундаментальных исследований: история математики.)

ISBN 5-354-00714-3

 

 

[5]

 

 

§ 1. В настоящей заметке делается попытка истолковать мнимые величины, не выходя при этом из первоначальных посылок аналитической геометрии на плоскости. А далее, в одном иа последующих параграфов, будет показано, что предлагаемое истолкование может быть применимо и вообще к двухмерным образам на кривых поверхностях, т. е. введено в дифференциальную геометрию.

Существует несколько способов подойти к мнимостям. Из них на первом месте должна стоять, конечно, формально-арифметическая установка комплексных чисел посредством Гамильтоновских двоиц, как наиболее абстрактная. Затем идет оперативная установка комплексов, как символов операций, и, близкая к ней, установка векторная. В качестве дальнейшего конкретного оплотнения двух последних установок следует рассматривать то семейство теорий, весьма близких между собою, но не абсолютно тождественных, в котором самая плоскость делается носительницей комплексных точек. Эти теории возникали самостоятельно неоднократно; привычнее многих других имен связываются с ними имена О. Коши. (1821,1847), Гаусса (1799) и женевца Р. Ж. Арганда. (1806); но мысль о подобной установке мнимостей уходит своими корнями и в более глубокое и более широкое прошлое: так, в этом отношении не должны быть обойденными имена прусского

 

[6]

 

геометра Генриха Кюна (1750), нашедшего приют своему мемуару в Записках С-Петербургской Академии Наук, датского математика Каспара В е с с е л я (1797), аббата Бюэ (1806), эльзасца Франсэ (1813—1815), француза Мурейя (1828), англичанина Джона Уарррена (1828), италианца О. Беллавитиса (1882), француза Гоюэля (1867), португальца Ф. Гомеса Техейры (1888) и многих других ¹.

В этом логическом преемстве ряда теорий без- сдорно проходит один, постепенно конкретизирующийся, замысел; было бы несправедливым и вредным пытаться разрушить выработанное многими совокупными усилиями орудие анализа, столь полезное при изучении функций мнимого переменного. Но не следует при таком признании обычного истолкования мнимостей забывать, что, все же,—это есть не более как интерпретация, символически являющая, но не исчерпывающая соответственных ариеметических сущностей. Плоскость комплексного переменного не есть еще самое переменное,—а лишь одно из истолкований такового на языке пространственных образов, и, следовательно, разделяющее с прочими истолкованиями присущие таковым формальные свойства². Ведь, всякое истолкование подлежит тому, что сказано Г. Герцем картинах мира: это есть система образов, ваятых произвольно, но соответствующих системе истолковываемой, и притом так, чтобы возможно большее число следствий из принятых истолковывающих образов соответствовало последствиям системы истолковываемой. Мы заранее внаем, что ни при одном способе толкования такой параллелизм следствий не может итш беспредельно далеко; мы не нуждаемся в доказательствах того, что перевод не покрывает подлинника во всех его оттенках и деталях, и загодя убеждены, что рано или поздно настанет такое их расхождение, которое не терпимо в пределах требуемой точности совпадения: всякий символ с успехом применим лишь в определенной, свойственной ему сфере, и за пределами известного поля

 

[7]

 

зрения расплывается, теряет четкость и скорее мешает работе, нежели помогает ей. Мы знаем и то, что, как несколько переводов поэтического произведения на другой язык или на другие языки не только не мешают друг другу, но и восполняют друг друга, хотя ни один не заменяет всецело подлинника, так и научные картины одной и той же реальности могут и должны быть умножаемы—вовсе не в ущерб истине. Зная же все это, мы научились не попрекать то или другое истолкование за то, чего оно не дает, а быть ему благодарным, когда удается использовать его.

Однако, к указанию ограниченности известной интерпретации мы вынуждаемся, коль скоро наблюдается ишертрофия того или другого перевода, пытающегося отождествить себя с подлинником и заменить его собою, т. е. тем самым монополизирующего некоторую сущность и ревниво исключающего какое-либо иное истолкование: тогда ничего не остается, как напомнить зазнавшейся интерпретации о приличном ей месте и объеме ея применимости.

Так именно обстоит дело с комплексной плоскостью Кюна—Весселя—Арганда—Гаусса—Коши. Конечно, она есть прекрасное пособие для изображения комплексного переменного и функций его,—впрочем недостаточное, как показывает необходимость введения поверхностей Риманна. Но это пособие отвечает определению функций, ведущему свою родословную от Л. Дирихле, т. е, посредством понятия о соответствии, и, конечно, недостаточному: ведь это определение, принимая во внимание лишь содержание («материальную причину») функции, проходит мимо главного, мимо самой функций, как целого, как формы, связующей это содержание воедино («формальная причина»). Тут не место говорить, сколько зла произошло и происходит от такого определения функции; не место говорить и о попытках перейти к иному образу понимания—развитием функционального исчисления, теории интегральных и интегро-дифференциальных уравнений, учением о функ-

 

[8]

 

циях линий и линиевых уравнениях. Но и в пределах теории функций, поскольку речь идет о функциях действительного переменного, зло от определения Дирихлэ отчасти ослабляется контрабандно вносимою поправкою в виде интуитивно представленной формы функции, как над-атомистического начала: имею в виду истолковывание течения функции посредством некоторой кривой. Когда же речь заходит о функциях переменного комплексного, то атомистичность сказанного определения выступает в полной силе. Ведь в теории функций комплексного переменного вся плоскость занимается под изображение переменного независимого, и потому переменному зависимому ничего не остается, как разместиться на самостоятельной плоскости, решительно ничем не связанной с первой. И потому, хотя мы и утверждаем, что будто точки на этой второй плоскости изображают зависимое переменное, однако, именно только утверждаем, но ничуть не показываем и не доказываем, ибо то, что одно только и могло бы геометрически показать и доказать эту зависимость,—самая связь двух переменных,—остается никак не представленной геометрически и, в порядке  геометрическом, т. е. в порядке самой интерпретации, есть голословное утверждение, лежащее вне возможности проверки, т. е. геометрически не существует. Повторяю, принятая интерпретация мнимостей в теории функций комплексного переменного интерпретирует лишь переменные, но отнюдь не самые функции, и в этом смысле может быть признана полезным, но далеко не достаточным, костылем анализа,—именно анализа и только его. Аналогичное должно быть повторено и о сфере Нейманна. А между тем, наряду с использованием геометрии в анализе, существует и должно существовать обратное использование анализа в геометрии, будь то геометрия аналитическая, дифференциальная или еще какая иная. И вот тут-то плоскость комплексного переменного никак не применима, ибо она порывает с установленными здесь и притом вполне естественными методами и ни-

 

[9]

 

как с ними не соизмерима. А между тем, и в геометрии мнимостй появляются не случайно, но необходимо связаны с формулировкою ея теорем и процессами ея доказательств, хотя здесь и не имеют геометрической наглядности. Уже в элементарном курсе аналитической геометрии, учащийся сплошь и рядом сталкивается с мнимыми образами, но, не будучи в состоянии дать им конкретно - воззрительное содержание, принужден трактовать в высшей степени обобщающие термины, вроде например «мнимой точки», чисто - формально, тогда как на то и существует геометрия, чтобы знанию не быть оторванным от пространственного созерцания. Хотя и аналитическая, однако, все же геометрия, аналитическая геометрия превращается наполовину в анализ, и притом так, что вся изрешетчивается пробелами, лишенными геометрического смысла: на каждом шагу тут, эа сплошь геометрической фразеологией, попадаются разрывы геометрической картины, и такое истолкование анализа, какое дает аналитическая геометрия, напоминает перевод с китайского языка, оставивший непереведенными и лишь транскрибированными помощью русских букв добрую половину иероглифических знаков. Можно сказать, что аналитическая геометрия уже не аналитична, как внесшая ряд пространственных  истолкований, и еще не геометрия, как не переведшая всего своего аналитического содержания на геометрические образы. Но ведь очень многие положения аналитической геометрии не имеют существенной важности, как аналитические, и ценны—именно как геометрические; усмотреть их пространственный смысл (а не утверждать таковой только на словах)—дело первостепенной важности. Правда, математика, привыкшего ко всяким «мнимым эллипсам», «циклическим точкам «изотропам» ит. п., в силу привычки (но отнюдь не вследствие понимания) подобная фразеология давно уж перестала беспокоить. Но эта успокоенность едва ли может рассматриваться, как источник развития математики. Учащийся в этом отношении более прав, когда

 

[10]

 

он чувствует в подобных высказываниях нечто недоговоренное. Определение окружности бесконечно- малого радиуса—как пары мнимых прямых» пересекающихся в действительной точке, центре окружности, представляется учащемуся—сперва блестящим парадоксом; а когда подобных понятий накопляется много, вся их совокупность раздражает, как приевшиеся остроты.

Итак, комплексная плоскость Коши—сама по себе, а мнимости, в аналитической и прочих геометриях,— сами по себе, и с ними обстоит неблагополучно, а вышеозначенное истолкование помочь тут никак не способно, и лишь запутывает налгу мысль, раздвояя ее между плоскостью, как носительницей самых функциональных связей, т. е. кривых, как это делается в аналитической геометрии и в теории функций действительного переменного, и плоскостью—носительницей одного только переменного, как такового, вне его связи с другим переменным, как об этом говорит теория функций переменного комплексного. Возникает задача: отправляясь от определения точка на плоскости двумя координатами (или соответственно тремя однородными) и понимания кривой на плоскости, как наглядного образа функциональной зависимости между текущими координатами точки ея, и не внося далее никакого разрыва в обычное изложение аналитической и прочих геометрий, расширить область двухмерных образов геометрии мак, чтобы в систему пространственных представлений вошли и мнимые образы. Короче говоря, необходимо найти в пространстве место для мнимых образов, и притом ничего не отнимая от уже занявших свои места образов действительных.

Или, говоря еще иначе, нужно, оставив без внимания все истолкования мнимостей, вернуться к формальной установке комплексных чисел и посмотреть, не допускают ли формально-необходимые, т. е. конститутивные, свойства комплексных чисел и иной, нежели исторически выработалась, линии истолкования. На это,

 

[11]

 

может быть, последует замечание о нежелательности разрыва с традицией, насчитывающей до пяти двад- цатипяти-летий, Да, это нежелательно; но еще более нежелателен разрыв с традицией, имеющей за собою до одиннадцати таких же промежутков времени. «Открытие Гаусса-Коши дало очень много >,—скажут- вероятно. Да, но еще более дало открытие Декарта и примыкающая к нему теория действительного переменного. С кем-то из двух, если не поссориться, то охладить отношения, приходится силою вещей, ибо эти двое— не в ладах между собою. А если так, то не пожертвовать ли ради Декарта и геометрической сообразности исключительностью в верности Коши?

 

 

§ 2. Итак, обращаемся к формальной теории комплексов. Они вводятся здесь посредством Гамильто- невских символов вида (ɑ, b), разработанных Вейерштрассом³ Самой основной, самой конститутивной характеристикою их является, конечно, именно их деоич- ность. Комплексы образуют множество двукратное, множество двояко-протяженное. Эту двоичность их конституции обычное истолкование приурочивает к двухмерности координатной плоскости. Но мы не можем сделать такого шага, потому что двукратная протяженность плоскости уже использована под интерпретацию функциональных зависимостей, и снова обращаться к тому же свойству плоскости—это значит нарушить jus primi occupantis,—в данном случае Декарта. Нам кажется, однако, что и Декарт и Коши впали в одну методологическую ошибку, которая, несмотря на свою кажущуюся маловажность, была чревата и логическими и практическими последствиями. Ошибка эта—в неправильном принятий единицы основной меры. В самом деле, спросим себя, что именно изучаем мы в геометрии. В геометрии изучаем мы п р о с т р а н с т в о,—не линии, точки и поверхности, как таковые, а именно свойства пространства, выражающиеся ж в этих частных пространственных образованиях.

 

[12]

 

И значит, единицею меры мы должны брать не величину не однородную с изучаемым объектом, а величину однородную,—часть самаго пространства. В абсолютной системе мер, секунда есть отрезок самаго времени, как иервоосвовной реальности. Почему же, в отношении пространства, в основу не положена часть самаго пространства? Точно так же, плоская геометрия изучает самро плоскость (или вообще поверхность); плоскость есть ел предмету линии же и точки на ней—частные образования на ней, и потому единицею меры мы должны брать в геометрии на плоскости именно часть плоскости, линейную же единицу рассматривать в качестве ⁴ единицы производной. Естественно при изучении любого объекта выбирать первоосновную единицу для его измерения однородною с величиною измеряемой, и. лишь впоследствии можно придумать какие-либо единицы вторичные и разнородные с перво-основной, хота, быть может, в каком-нибудь отношении и более удобные практически. Таков логический путь, и пренебрежение им ведет к разным осложнениям.

 

 

Чтобы наши рассуждений были более конкретными, поведем их на совсем простых примерах.

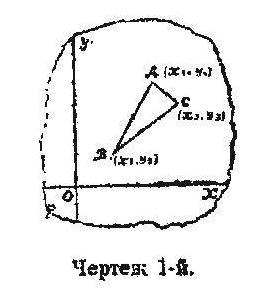
Пусть в плоскости Р дан треугольник ABC (чертеж 1-й); координаты вершин его, отнесенные к прямоугольным декартовым осям, суть:

Тогда, как известно, площадь его

 

Но ведь вершины его вполне равноправны меаду собою. Поэтому мы должны, повидимому, получить то же. если переименуем вершину В в С, а С в В.

 

[13]

 

Оказывается, что тогда площадь меняет свой знак, оставаясь ло абсолютной величине неизменною:

 

 

 

Иными словами,

∆₂ = - ∆₁  [3]

 

 

Почему же произошла такая разница? Почему, при перемене названий вершин, значение площади, абсолютную величину которой мы будем обозначать просто чрез ∆, изменило знак?—Потому, что мы совершаем теперь обход вершин в ином порядке» чем ранее. Оказывается, именно, что чертеж  если обход этот совершается против

часовой стрелки, то ∆ будет положительна, а если—по стрелке, то отрицательна (чертеж 2-й и чертеж 3-й).

 

 

Но площадь, как площадь, сама по себе не заключает еще, согласно обычному представлению, той полярности, которая дает величине возможность быть положительной или отрицательной. Хождение по прямой взад и вперед затрагивает самое содержание прямолинейного отрезка, ибо при таком хождении мы имеем дело со всеми его элементами и притом непременно только в одном из двух смыслов. О площади же сказать этого нельзя: ведь для нея возможны не два обхода, а бесчисленное множество обходов, например такой, какой изображен на чертеже 4-м, и обходы, вообще говоря, не могут затронуть всех точек плоскости; даже кривые вроде кривой Пеано и т. п., исчерпывающие есе точки площади, не могут быть рассматриваемы как полярно-противоположные, ибо их может быть бесчисленное множество. Наш прежний ответ о причине изменения знака у площади был чисто формальным и только тавтологически повторял вопрос, потому что

 

[14]

 

говорить об изменении смысла движения и о порядке проходимых при этом вершин—это одно и тоже. Площадь, как таковая, обходом ея периметра не характеризуется, и не это хождение посолонь или против солнца может внести двойственность. Причину этой двойственности нужно искать в другом, глубже.

 

 

Рассмотрим, как может быть получено изменение знака площади у данного треугольника.

Раз абсолютная величина площади не меняется и не меняются углы и стороны треугольника, то, значит, при этом процессе изменения знака треугольник сохраняется, т. е. движется, как одно целое. Действительная причина изменения знака площади есть какое-то движение треугольника, а не простое переименование вершин.

Прежде всего исследуем движения треугольника в плоскости Р (чертеж 1-й), при Чем ради общности и изящества результатов будем пользоваться трилинейными координатами и движениями не только обычными, но и такими, при которых образ изменяется подобно себе. При указанных условиях, если мы обозначим координаты вершин чрез x_Ʀ1 у_Ʀ1 z _Ʀ1 (где Ʀ =l, 2, 3), площадь ∆ выразится так:

 

 

Будем совершать всевозможные коллинеации, даже такие, при которых детерминант замещения D не равен 1. Формулы преобразования при этом таковы:

 

 

[15]

 

Вставляя девять величин из формул [5] в выражение [4], мы найдем:

 

 

где C  есть постоянное,

 

 

Раскрывая выражение ∆ в равенстве [7]  и делая приведения, мы получаем, cогласно известной теореме о произведении определителей:

∆ = M. D. ∆′    [9]

где D есть детерминант замещения:

 

 

а ∆ ^/    есть площадь преобразованного треугольника:

 

 

Следовательно, площадь треугольника инвариантна при всех коллинеациях: площадь треугольника есть образование инвариантное при всех линейных преобразованиях.

А так как всякую площадь, ограниченную ломанной замкнутой линией, можно разбить на сумму треугольников, то и всякая площадь, ограниченная ломанным периметром, составленным из прямолинейнее звеньев, инвариантна. Переходя, далее, к пределу, мы можем сказать, что и всякая криволинейная площадь, ограниченная каким угодно контуром, инвариантна при всех коллинеациях

[16]

 

Ограничиваясь теперь такими коллинеарными преобразованиями, для которых

|D.M = 1|  [12]

т. е. истинными движениями образа, как неизменяемой геометрической системы, мы замечаем следующее:

1. При таких преобразованиях абсолютная величина площади не меняется:

 

|∆ ^/ | = |∆ |  [13]

 

2. Знак площади может быть как положительным, так и отрицательным, в зависимости от знака при D или при ∆, тогда как знак М существенно положителен»

Знак детерминанта замещения D не может не быть, в случае истинных движений, положителен; в противном случае, всякое, даже бесконечно-малое перемещение треугольника меняло бы знак площади, а это не соответствовало бы непрерывности движения. Вариируя координаты вершин треугольника, т. е. заменяя

 

 

по непрерывности детерминанта, как функции его элементов, мы не можем переменить его знака, иначе, как проходя чрез нуль, а нулем площадь треугольника стать не может. Следовательно, при коллинеарных преобразованиях площадь не меняет своего знака. А, следовательно, знак детерминанта замещения должен быть положителен, т. к. в противном случае и знак,—какова бы ни была вариация,—непременно менялся бы.

 

 

§ 3. Коллинеарные преобразования площади не меняют ея знака, по крайней мере покуда они имеют кинематический смысл движений в пределах рассматриваемого плоского пространства. Но это не значит, чтобы такое изменение знака было вообще невозможно. Предположим, что мы подняли рассматриваемый треугольник AВС над плоскостью Р, т. е., воспользовавшись третьим измерением пространства, перевернули треугольник и снова положили плашмя на плоскость P (чер-

 

[17]

 

теж 5-й). То же самое можно представить себе иначе: пусть в плоскости Р треугольника АВС дается некая ось zκ. Соединяя треугольник неизменяемой связью с осыо и нращая плоскость треугольника и связи на угол 2π мы заставим треугольник снова лечь на плоскость Р. Но теперь уже он будет лежать не прежней стороной, а оборотного. Легко видеть, что площадь его изменила свой знак, потому что изменилось на обратное—направление обхода площади. Следовательно, переворачивание в третьем измерении и есть искомое движение, меняющее знак площади треугольника, а, по сказанному ранее,—и площади всякой фигуры вообще.

 

 

В данной работе не станем касаться того существенно-важного обстоятельства, что от такого движения получается треугольник, или вообще фигура неконгруэнтный с данным первоначально. Эта нековгруэнтность равных геометрических образов имеет, как известно, чрезвычайно важное значение в философии и а естествознании, что уже отчасти пояснено работами Рене де Сосюра и механикой многомерных пространств, а также и многими другими, чему надлежит посвятить особое исследование.

Но возвращаемся к нашему треугольнику. Площадь его, а равно—и всякой фигуры, имеет знак положительный или отрицательный, в зависимости от того, какая сторона такой фигуры изучается. Конечно, для плоских фигур нет существенного различия между двумя сторонами их (исключая неконгруентность при как бы разделении сторон и переворачивании одной из них); но, если дело пойдет о кривых поверхностях, то различие фигур на выпуклой и на вогнутой, или, шире,

 

[18]

 

вообще—на разных сторонах поверхности, приобретает важное значение и пеусловное содержание (в частности, с такими свойствами геометрических образов имеет дело сферическая тригонометрия). Точнее говоря, подобное же различение в отношении плоскости должно рассматриваться как переход к пределу, при постепенном уменьшении кривизны поверхности до нуля.

До сих пор мы меняли положение фигуры относительно наблюдателя. Но, вместо этого, мы можем заставить самого наблюдателя перемещаться относительно фигуры, т. е. рассматривать фигуру на плоскости с разных сторон. Тогда мы уже не будем говорить, что изменяется положение фигуры, ея размеры или направление обхода на ней. Последнее, т. е. смысл (sens) обхода, дано абсолютно. Абсолютность смысла обхода мы осуществим, если г самою фигурою будет связано некоторое циклическое движение, неизменное по своему смыслу, какое бы положение ни занял наблюдатель его. Например, мы могли бы поместить на фигуру часы с прозрачным циферблатом или шарик, обегающий контур фигуры, или по контуру фигуры пустить электрический ток; смысл «тих движений был бы независим от положении наблюдателя, и потому, зная этот смысл, как установленный рал навсегда, наблюдатель мог бы ориентироваться в своем отношении к той или другой стороне плоскости. Итак, пусть этот абсолютный обход, раз на всегда установленный, считается положительным, когда он видится протекающим против движении часовой стрелки, и—положительным. когда видится он протекающим по этому движению. Или, иначе, если наблюдатель находится па положительном конце нормали к поверхности, то обход контура непременно совершается против часовой стрелки; а если обход видится происходящим по часовой стрелке, то это значит, что на пего наблюдатель смотрит с отрицательного конца нормали. При таком рассмотрении плоскости весьма выгодны координатные оси Максвелла

 

[19]

 

чертеж 7-ой). Допустим теперь, что мы перешли на отрицательный конец оси Z и смотрим оттуда на наш треугольник. Тогда, при том же самом абсолютном обходе его периметра, мы увидим, что обход совершается против часовой стрелки. Если тогда, ранее, мы считали, по декартовским координатам, площадь обходимого контура положительной, то теперь, при том же обходе, сочтем ее отрицательной, но, переменив систему осей на максвел-левскую (чертежи 6-й и 7-й),

 

 

мы должны говорить наоборот, и о прежней площади рассуждать, как об отрицательной, а о теперешней—как о положительной.

 

Таким образом, всякий вырезок плоскости с одной стороны положителен, а с другой — отрицателен, и потому вся плоскость с одной стороны положительна, а с другой отрицательна. Сторона плоскости характеризуется знаком любой, вырезанной из плоскости, площадки. Плоскость стала как бы прозрачна, и когда мы видим на ней площадки разных знаков, то это, теперь уже, должно быть относимо не за счет разного смысла их обходов, каковой может быть только одним, абсолютным, а за счет различных сторон плоскости, к которым и приурочиваются рассматриваемые площадки.

 

 

§ 4. Прежде, чем итти далее в рассуждениях геометрических, кажется, будет небесполезным несколькими примерами напомнить физический смысл устанавливаемого понятия о полярности плоскости» как геометрического образа, к которому применимо различение величин положительных и отрицательных, аналогично подобному же различению на линии. Разница с линией— в том, что знак относится там к содержанию линии, как тиковой, т. е, к отрезку линейному, а тут—к co-

 

[20]

 

держанию плоскости, как таковой, т. е. к плоскостной величине, к площади Следовательно, всякое физическое явление, которое может быть изображаемо вырезками плоскости и которое полярно, в устанавливаемом здесь понятии о знаке плоскости получает себе полезную диаграмму. Сюда же относится всякий процесс , могущий быть графически изображенным некоторым обходом, имеющим определенный смысл, или, еще, внутреннюю противоположность своего смысла, заставляющую в диаграмме его воспользоваться возможностью двоякого направления обхода. Вот несколько простейших примеров:

I.Магнитный листок, т. е. поверхность, по которой, нормально к ней, щетиною, расположены бесконечно-малые магнитики, есть физическое осуществление геометрического образа плоскости, или, как увидим далее, вообще поверхности двусторонней. Потенциал такого листка или, лучше, его элемента, поверхности dS будет положителен или отрицателен, смотря по тому, будет ли видна из места наблюдения положительная или отрицательная сторона элемента dS. (Чертеж 8-й).

 

 

II. То же самое можно сказать о двойном электрическом слое.

III. Правило Амперовского пловца и правило Максвеллева штопора относительно направления магнитных силовых линий тока («направление тока и направление магнитной силы его связаны между собою так же, как направление поступательного и вращательного движения обыкновенного винта или штопора») показывают, что плоскость, рассекающая ток перпендикулярно к нему, имеет по существу различные стороны, хотя бы например потому, что северный Полюс на одной стороне будет двигаться по часовой стрелке, а на другой—против нея, что поля-

 

[21]

 

рисованный луч повернется там и тут в противоположные стороны и т. д.

IV. Теорема Ампера об эквивалентности замкнутого тока и соответственного магнитного листка, имеющего тот же контур (чертеж 9-й), приводит к рассуждениям. подобным тем, что в пункте I.

V. Теоремы об индукции, где направление тока обусловливается тем, входят иди выходят силовые линии в контур с его положительной или отрицательной стороны, опять возращают мысль к тому же различению знака у плоскости.

 

 

VI. Положим, что в ванне с электролитом, в которой проходит ток, находится проводящий лист, разделяющей электроды. Он поляризуется, и тогда, как бы тонок он ни был. стороны поверхности его представят существенное различие, так что к ним, опять, будет весьма выгодно применить представление о  знаке плоскости (чертеж 10-й).

 

 

VII. Рассмотрим Тэтовскую диаграмму термоэлектрических явлений. Напомним те два закона, на основании которых она построена:

 

[22]

 

 

Здесь Е означает электровозбудительную силу данной пары металлов из числа А, В, С,...X. Пределы асе t₁, t_{2, ϐ} обозначают температуры спаев. Тэт строит такую кривую, чтобы площадь между осью абсцисс, кривой и двумя бесконечно - близкими ординатами, соответствующими «термоэлектрической способности» φ(АХ) при соответствующих температурах (абсциссах). была пропорциональна электровозбудительной силе термоэлемента. Тогда эта кривая относится к металлу А, а ось абсцисс к металлу X (чертеж 11-й). На основании второе закона [15], площадь трапеции MM"N"N представит собою электродвижущую силу пары (MN).

 

 

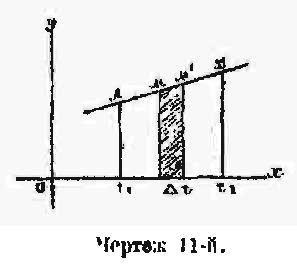
Если температуру холодного спая ОР мы оставляем неизменной, а температуру теплого увеличивши до OР" то (чертеж 12-й) Е тогда достигает наибольшего значения; после этого начнется убывание Е до нуля, причем этому значению Е соответствует температура ОР"ʹ такая, что РР"= Р"Р"ʹ после чего происходит явление инверсии, обращение тока. Такова диаграмма. Сперва может показаться странным, почему происходит так. ибо площадь, изображающая электродвижущую силу, как будто продолжает возрастать, между тем как электродвижущая сила убывает. Но дело в том, что после пересечения кривых в точке К площадь становится отрицательной и, следовательно, уже не прибавляется к площади, бывшей до К, а вычитается из нея.

 

 

[23]

 

Подобных примеров из самых различных областей. где находит себе место полярное представление плоскости, можно привести много; но, полагаю, и сказанных достаточно, чтобы сделать себе физический смысл этого представления наглядным. Аналитически дело сводится к возможности выразить потенциальную функцию двойного слоя посредством некоторого интеграла по контуру этого слоя. т. е. к частному случаю более общей теоремы Стокса_у дающей тождественное равенство двух интегралов, поверхностного и контурного, так что изменение смысла обхода в последнем— необходимо связано, следовательно, с изменением знаки у каждого элемента площади ⁴.

 

 

 

[S] = [Lʹ]    [17]

 

Если длину считаем мы за величину первого измерения, измерения 1, то тогда площадь должна рассматриваться, как величина второго измерения, как величина измерения 2. А т. к. в наглядном созерцании мы :шаем длины лишь положительные и отрицательные, то, при вышеозначенной точке зрения, пришлось бы утверждать, что площади могут быть только положительные. Однако, мы видели, полную геометрическую наглядность н отрицательных площадей. Отсюда следует, что дри изучении плоскости не правильно принимать площадь за величину второго измерения, а длину— перв ого. Мы уже видели в § 1 методологическое требование принимать за основную

единицу, т. е. единицу первого измерения, часть того объекта, который нами изучается, чтобы в самом определения меры не было логической ошибки — логического уравнивания понятии заведомо разнородных.

 

[24]

Будем рассуждать конкретно. Вырежем на плоскости квадрат, площади b единиц. Это b может быть как положительным, так и отрицательным. Рассмотрим же тот случай, когда b отрицательно. Тогда, чтобы площадь была отрицательной, необходимо, чтобы сторона квадрата была положительной или отрицательной мнимостью (чертеж 14-й):

 

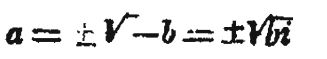
   [18]

 

 

Итак, сторона квадрата отрицательной площади мнима. Двойной знак ем указывает на то, что направление этой стороны может братье» как в одну, так и в другую сторону,—как это вообще делается в аналитической геометрии.

Таким же, следовательно, т.е. мнимым, должен быть и всякий отрезок прямой, всякая длина на ни жь е й с т ор о н е п л о с ко схн (если верхняя положительна), всякий линейный элемент, а потому—и длина всякой дуги, как предел суммы прямолинейных звеньев периметра вписанной в дугу ломанной.

Но, если мнимым будет всякий отрезок нижней стороны плоскости, то мнимыми будут и кординаты любой точки на нижней стороне плоскости. Поэтому, точку оборотной стороны, т. е. с мнимыми координатами, мы станем называть точкою мнимою. Однако, требуется оговориться относительно этого названия, не совсем совпадающего с общепринятым, т. к. обыкновенно «мнимою точкою» называют точку с координатами комплексными, тогда как мы имеем в виду чисто-мнимые величины, вида ±bi. Кроме того, иногда термин «мнимая точка , с мнимая ветвь кривой , относят к таким точкам или ветвям, у которых одна координата мнима или комплексна, тогда как другая (обыкновенно абсцисса),—действительна. В подобных случаях мы будем говорить о полу-мнимости.

 

[25]

 

т. е. о пол у-мнимых точках и полу-мнимых ветвях кривой.

Ради сохранении однородности измерения величии, необходимо и цлощадь на положительной стороне плоскости считать величиною первого измерения, а всякий отрезок на ней — величиною измерения ½, потому что он получается чрез извлечение корня квадратного из 1.

Итак, если у нас есть квадрат с площадью +b и квадрат с площадью -b, то сторона первого квадрата будет 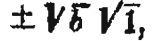,  а второго будет  Так сохраняется однородность величин, по существу однородных, и не вносится, практически, никаких изменений в обычное трактование положительной (доселе только и бывшей известной) стороны плоскости: теперь мы должны только мысленно заменять выражение «столько-то основных единиц , выражением «столько-то основных единиц в степени ½».  Новая интерпретация мнимостей заключается в открытии оборотной стороны плоскости и приурочении этом стороне—области мнимых чисел. Мнимый отрезок относятся, согласно этой интерпретации, к противоположной стороне плоскости; там находится своя координатная система, в одном случае совпадающая с действительной, а в другом—расходящаяся с нею. Для нас теперь, повторяем, плоскость стала прозрачной, и мы видим обе системы осей зараз, так что можем представить плоскость так, как это сделано па чертеже l5-м, где пунктиром проведена мнимая система осей.

 

 

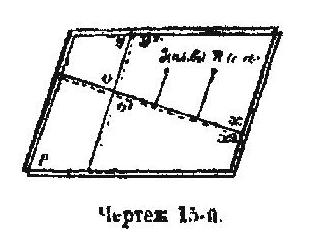
Возвращаясь, с разъясненной точки зрения, к площади треугольника, об инвариантности которой шли рассуждения в § 2, мы можем понять, как, при положительном детерминанте замещения D, равном единице, т. е. при коллинеациях. соответствующих настоящим движениям, площадь все же может изменить свой знак. В самом

 

[26]

 

деле, подставляя в выражение для площади |8| мнимые координаты ix_Ʀ и iy_Ʀ (Ʀ=1, 2, 3) вершин, и вынося мнимую единицу i за зпак детерминанта, мы получаем действительную величину детерминанта, равную площади треугольника с соответствующими действительными координатами вершин, но имеющую противоположный знак: мнимое преобразование координат переменило смысл обхода, ибо перевернуло треугольник плашмя, перевернуло же потому, что перенесло его на отрицательную сторону плоскости.

 

 

и следовательно

∆ʹ = - ∆    [20]

 

Для определенности дальнейших рассуждений подведем итоги и дадим несколько определений:

I. Действительная точка есть такая точка; обе координаты которой действительны: R (ɑ, b). Она лежит на положительной стороне плоскости (на чертеже— верхней) и определяется пересечением двух прямых на положительной стороне плоскости.

II. Мнимая точка есть такая точка, обе координаты которой мшшы. R(ɑi, bi). Определяется мнимая точка двумя прямыми на отрицательной стороне плоскости, на чертеже—оборотной.

III. Всякая прямая, проходящая через две действительные точки, есть прямая действительная. Она расположена на верхней стороне плоскости, и уравнение ея удовлетворяется действительными точками.

IV. Всякая прямая, проходящая чрез две мнимые точки, есть прямая мнимая. Она расположена на отрицательной (нижней) стороне плоскости, и уравнение ея  удовлетворяется точками мнимыми.

 

[27]

 

§ 6. Алгебраические действия над комплексными числами приводят, в итогй, к комплексам же и только к ним. Поэтому, координаты точек, полученные из уравнения любой плоской кривой, могут быть либо действительными, либо чисто-мнимыми, либо комплексными, — и никакими иными, — иначе говоря только одного из нижеследующих трех типов: ɑ, ɑi, a+bi, где ɑ и b суть действительные числа, положительные или отрицательные. Следовательно, из различных сочетаний координат этих трех типов возникает возможность девяти различных видов точек плоскости, как она рассматривается в аналитической геометрии,—и только их; эти девять видов распадаются на шесть существенно различных родов:

 

 

Сочетания, соединенные скобкою,относятся к точкам, подобным между собою, но с измененными названиями координат.

Таковы шесть родов точек плоскости (обращаем внимание, что сказано «плоскости» а не «на плоскости»). Никакие операции анализа не дадут чего-либо, неизобразимого этими точками; и следовательно, для точного совпадения анализа и геометрии нужно только дать наглядность всем точкам. До сих пор выяснился геометрический образ, соответствующий как действительным, так и мнимым точкам; требуется же теперь геометрически приспособить прочие четыре рода. Начнем с точек полу-миимьтх.

 

[28]

 

Пусть в пространстве даны какие-нибудь две примы я. Вообще говоря, оне не пересекаются между собою, но тем не менее между ними существует кратчайшее расстояние,—общий иx перпендикуляр. Эта линия единственна; поэтому мы можем сказать, что две прямые вполне характеризуют некоторый отрезок (кратчайшее между ними расстояние) и на нем—некоторую точку, которая хотя и может двигаться по отрезку, но лишь в известной области, между прямыми (чертеж 16-й),

 

 

т. е. между точками А₁ и А₂. Станем сближать между собою прямые. Тогда область произвольности А₁А₂ точки А становится все теснее, и в предела точка делаете я вполне определенною, именно обращается в точку пересечения двух линий и сливается с А₁ и А_2. Но, как ранее точка А все время находилась между данными линиями, так и о предельном случае мы можем продолжать говорить, что А—м е ж д у линиями (чертеж 17-й). Представим себе далее (чертеж 18-й),

 

 

 

 

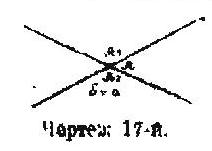
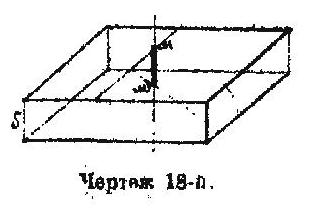
что у нас, вместо бесконечной плоскости,—бесконечная пластина, — слой переменной толщины с параллельными гранями. Чертежем представлен вырезок из этого слоя. На одной стороне этого пласта проведем одну лиийю. на другой —другую. Отыщем, далее, кратчайшее расстояние обеих линий: оно будет равно δ и направлено нормально к граням. Делаем, теперь, толщину слоя δ все меньшей и меньшей. Тогда каждая линия, оставаясь на той стороне пласта, на которой она начерчена, станет приближаться к линии, чтб на другой стороне. В пределе, когда обе грани сольются, пересечение линий на разных сторонах плоскости, получившейся как предел вышеозначенного пласта, определит собою не-

 

[29]

 

которую точку. Точка эта будет полу-мнимой, ибо чрез нее проходит одна прямая действительная и одна мнимая, которые могут быть сочтены за косоугольные координаты ея; в частном случае, эти прямая могут быть перпендикулярными между собою и параллельными осям. А что одна из этих прямых, именно нижняя, будет мнимою, другая же, верхняя,— действительною, это явствует из разъяснений, сделанных ранее. Полу-мнимая точка находится между проведенными линиями, стало быть, - емежду тех граней, на которых означенные линии проведены. Значит, действительные точки расположены сверху, мнимые—снизу;, те и другие на соответствующих сторонах, а полу-мнимые—внутри, в самой плоскости, между ея сторонами. Но было уже сказано, что полу-мнимая прямая проходит чрез две полу-мнимые точки; следовательно, она также лежит внутри плоскости, между ей гранями.

Всякий геометрический образ—геометрическое место точек—назовется мнимым, полу-мнимым или действительным, смотря по тому, какие точки лежат на этом «месте», мнимые, полу-мнимые или действительные. Действительный образ чертится, как обычно, на верхней стороне плоскости; .мы станем обозначать его сплошною линией. Полу-мнимый—чертится внутри плоскости, и обозначением его будет пунктир. Наконец мнимый образ должен чертиться на нижней стороне плоскости; а на верхней, как бы просвечивая, он пусть обозначается черточками (чертеж 19-й).

 

 

Теперь осталось рассмотреть точки полу-комплексные, точки комплексные и точки мнимо-комплексные, т. е. те, координаты которых суть:

 

 

[30]

 

Пусть дана точка М (ɑ, b+ci). Чтобы построить ее, надо (чертеж 20-й)

 

 

ваять линию, параллельную оси ординат, на расстоянии ɑ, и найти ее пересечение с параллелью оси абсцисс, на расстоянии b+ci. Это значит, что надо взять по оси Y отрезок b на верхней плоскости, затем от конца b отложить на нижней стороне ci и провести через конец так полученной суммы линию, параллельную оси X. Точка пересечении этой линии с линией, проведенной раньше, будет М_1. Но ведь мы могли бы по- <тупить и иначе: сначала взять па оси У отрезок ci, а затем уже b, и тогда получилась бы точка пересечения М₂ на том же месте, что и М₁, но не в том же отношении к сторонам плоскости. Тут точка была бы действительной, тогда как ранее она была полу-мнимой. Между тем, искомая точка М должна быть единственной. и этой единственности ей можно добиться, если тот п другой образ ен, действительный и гтолу- мнимый, считать вместо за одну точку, Вместе оне образуют одну точку, одновременно находящуюся на верхней стороне плоскости и между сторонами ея. Если переход к пределу еще не совершен, т. е., если δ ≠ 0, и вместо плоскости у кас все еще пласт, то можно уподобить пол у-коль плексную точку М гвоздю, во-гнанному до половины глубины в этот пласт. (Чертеж 22-ой).

 

 

 

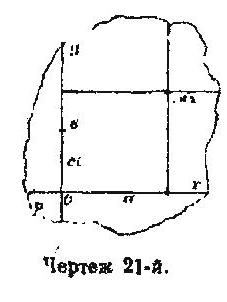
Остается, наконец, рассмотреть комплексную точку М (a+di, b+ci). Тут, при различной последовательности сложений, возможны четыре возможности; эти четыре

 

[31]

 

возможности приводят, как видно на чертежах 23, 24, 25, 26-ом,

 

 

 

к точкам: действительной, полу-мнимой, еще полу-мнимой и просто мнимой, находящимся на одном к том же месте пространства, но в разных отношениях к сторонам плоскости. Весь столбик четырех точек, из которых две—на наружных сторонах плоскости и две—на внутренних, внутри ей, образует одну точку М (a+di, b+di), так что мы ее можем представлять себе в виде штифта, проходящего чрез всю толщу пласта насквозь и выходящего на обратной стороне ея. Такой результат легко было бы предвидеть:  ведь, очевидно, что точка комплексная должна быть  представлена таким образом, чтобы при частных ограничениях, т.е. полагая действительные или мнимые компоненты   ея координат  нулю, мы могли получить из комплексной точки точку действительную, полу-мнимую и мнимую. Следовательно, комплексная точка объединяет в себе все частные виды точек, а плоскость Р есть носительница именно комплексных точек, тогда как прочие

 

 

[32]

 

точки суть образования на ней и в ней. Это—точки, как бы имеющие некоторую высоту. Поэтому, таковы же и линии, проходящие чрез подобные точки: линия прямая, проходящая чрез две комплексные точки, прорезывает плоскость насквозь; проходящая чрез две полу-комплексные точки, делает надрез с верхней стороны плоскости, а проходящая чрез две мнимо-комплексные точки надрезывает плоскость с нижней стороны. Если бы посмотреть на эти прямые в микроскоп при бесконечном увеличении, то мы увидели бы полоски, как это изображено на чертеже 28-ом; плоскость этих полосок— перпендикулярна к сторонам поверхности координатной плоскости.

 

 

Подобно прямым, н кривые линии, уравнение которых удовлетворяется комплексными, полу-комплекс - иыми или мнимо-комплекснымй точками, либо прорезают плоскость насквозь, либо надрезывают ее сверху или снизу. Бесконечно увеличенные в направлении нормальном к плоскости своей, оне представились бы цилиндрическими поверхностями, образующия которых нормальны к сторонам координатной плоскости. (Чертеж  29-й).  Выражаясь несколько условно, скажем: линии действительные, мнимые и полу-мйимые бесконечно ниже, нежели липии полу-комплексные и мнимо-ком- йлексные; а линии этих двух последних родов ниже, но не бесконечно, линий комплексных. Условность такого выражения—в том, что, конечно, ни одна линия не имеет высоты, или, иначе говоря, высота всякой линии равна нулю; но высоты линий, если брать их до перехода к пределу, стремятся к нулю с различною интенсивностью, с различною быстротою. Последнее вы

 

 

[33]

 

ражение заимствовано нами уБуссинеска, говорящего о дифференциале следующее: «Дифференциал не обозначает вполне, или, как говорят, об"ективно малой разности; он обозначает ее только субъективно, т. е,, по нашему понятию, обозначает ее напряжением, с которым мы заставляем ее стремиться к нулю и рассматриваем только пределы, к которым будут стремиться результаты исчислений. Идея, которую имел Лейбниц, заставить подобное напряжение фигурировать в формулах, так же проста, как и замечательна, т. к. она позволяет производить уничтожения, нисколько не нарушая правильности формул». Вот таким-то н а п р я ж ением и представляем мы себе высоту поверхности, точек и линий, И представление это необходимо,—несистематически же давно существует в науке: разве не так именно мыслятся в физике элементарные магниты, двойной магнитный и электрический слой и т. д. Полное отрицание за ними протяжения просто уничтожило бы их магнитное или электрическое действие, придание же их протяжению—конечных размеров нарушило бы элементарный характер этих образований. (Полагаю, что как применительно к этим физическим образованиям, так и в отношении разъясненных образов геометрических, следовало бы воспользоваться понятием актуально бесконе ч н о-м алых и что мы имеем право толковать толщину плоскости как отнюдь не нулевую величину, но— актуально бесконечно-малую, и, соответственно с этим,— толщину магнитного листка, двойного слоя и т. п. Но в настоящей работе, посвященной вопросам иного порядка, не считаю уместным входить в эти, доселе еще не доразрешенные, тонкие проблемы и потому довольствуюсь пока понятием о напряжении, хотя и вижу его логическую недостаточность).

 

[34]

 

§ 7.  Итак, согласно предлагаемому толкованию мнимостей, кривая может уходить с лица поверхности вглубь ея толщи и тогда протекает на том или другом участке своего течения на подобие подземных рек, изображаемых на карте пунктиром,—чтобы затем найти себе выход наружу. Это, с точки зрения поверхностных процессов на плоскости, есть качественное изменение хода кривой; но по существу оно не нарушает связности кривой, коль скоро она рассматривается как образ, хотя и плоский, но все же пространственный:

 

 

предлагаемое толкование дает возможность геометрически понять соотношение всех ветвей ея между собою.— На нескольких примерах поясним такое применение  предлагаемого толкования.

 

[35]

 

Пусть имеется уравнение гиперболы в каноническом виде:

 

 

которое можно переписать еще так:

Или

 

 

Тогда все ветви, выражаемые данным уравнением, как действительные, так и полу-мнимые, составляют своею совокупностью одну кривую. Пусть теперь величина полу-оси а остается конечной и неизменной, тогда как полу-ось b меняет свой размер, так что следовательно меняется и р. Теперь,

если то кривая распадается на пару прямых, параллельных оси У я проходящих на расстоянии ±ɑ от нея, причем каждую прямую надо считать парной, из слившихся действительной и полу-мнимой прямой;

если р>1, то образуется действительная гипербола, из пары ветвей, и полу-мнимый эллипс, соприкасающиеся в вершинах; по мере уменьшения b они будут сжиматься к оси Х; приравняв нулю левую часть уравнения [21], получим уравнение пары действительных ассимптот, касательных к действительным ветвям кривой;

если p = 1 то тогда действительные гиперболы становятся равносторонними, а полу-мнимый эллипс—полумнимою окружностью, ассимптоты же полу-мнимой окружности будут соответствовать изотропам действительной окружности;

если 0<р<1, то все ветви кривой еще более спадаются, полу-мнимый эллипс делается сжатым; в пределе,

если p = +0, то все ветви сжимаются в пару слившихся на оси X прямых; это—две спавшихся ветви бесконечно-

 

[36]

тонкой действительной гиперболы и бесконечно-тонкий полу-мнимый эллипс. Обычно говорят, что бесконечно-тонкая гипербола распадается на пару действительных прямых; но это неверно, ибо тут смешивается предельное значение (при р=+0) с значением на пределе (при р=0). На самом деле имеется здесь пара действительных отрезков, разделенных отрезком полу-мнимым;

если p=0, то вместо кривой образуется по оси X провал, щель; кривая, проваливаясь в нее, мгновенно выворачивается; то, что было на поверхности, входит в ея толщу, а что было в толще—выходит на поверхность, и потому,

если р=-0, то спавшаяся кривая представляет собою действительный средний отрезок (бесконечно-тонкий действительный эллипс) и полу-мнимые бесконечные придатки его (бесконечно-тонкая полу-мнимая гипербола);

если -1<p<0, то получается сжатый действительный эллипс и полу-мнимая сжатая гипербола;

если p = - 1, то эллипс превращается в действительную окружность, а гипербола делается равностороннею полу-мнимою гиперболой;

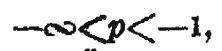
если  то окружность вытягивается в действительный эллипс, гипербола расширяется, оставаясь полу-мнимою и, наконец,

если то снова образуются две лары слившихся прямых, параллельных оси У и проходящих в расстоянии ±ɑ от нея, но теперь уже эллипс обращается в действительные прямыя, а гипербола—в полу-мнимые.

Такова связная картина всех превращений коники при изменении одной полу-оси.

 

Весьма наглядно, при пользовании предлагаемым толкованием мнимостей, поведение кривых в особых точках. Рассмотрим например простую кривую третьего порядка, представляемую уравнением

 

[37]

 

 

которое, ради удобства, можно привести к виду:

Течение кривой представлено на чертеже 31-ом. Как видно, принадлежность замкнутого овала в кривой обменяется существованием полу-мнимых ветвей, егр привязывающих

к кривой. Станем теперь менять величину параметров а, b, с:

если ɑ=b>с, то овал прилипает к кривой (чертеж 32-й);

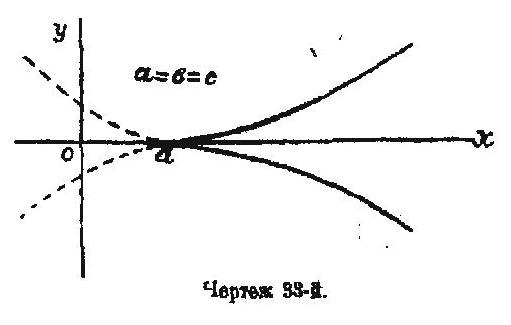
если а=b=c, то петля затягивается в точку, так что образуется точка возврата (чертеж 33-й);

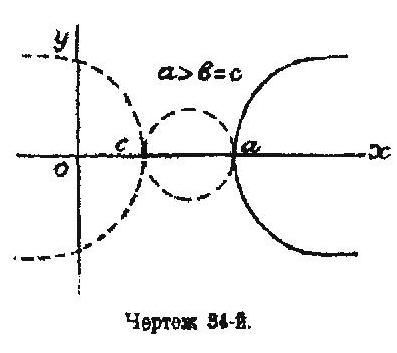
если b=с>ɑ, то овал, оставаясь отделенным от кривой или, точнее, висящим на полу-мнимых ветвях, затягивается в точечную петлю; это—изолированная точка, и понятно, почему ее должны мы рассматривать как принадлежащую к кривой, хотя она и кажется отделенной при обычном способе изображения (чертеж 34-й).

 

 

 

§ 8. Обобщение предлагаемою истолкования мнимостей с плоскости—на всякие поверхности.—Мы рассматривали доселе мнимости, как линейные протяжения на оборотной стороне координатной плоскости. Но так как основа интерпретации тут—в наличности оборотной

 

[38]

 

стороны, а не в характере кривизны данной координатной поверхности, то естественно распространить предлагаемую интерпретацию на всевозможные поверхности, рассматриваемые как носительницы гауссовых криволинейных координат на них. И тогда возникает необходимость уяснить себе, а как же, в таком случае,  должны быть  поняты поверхности односторонние.—По общему смыслу наших рассуждений, должно, но видимому, получиться, что на поверхностях односторонних мнимостей не бывает, или же что там—одне только мнимости. Но это заключение необходимо, конечно, провести аналитически. Можно было бы поставленный вопрос расширить и далее, воспользовавшись доказанным мною (в лекциях по «Энциклопедии Мате-матики», читанных в 1919—1920 академическом году в Сергиево-Посадском Институте Народного Образования) делением поверхностей на четно-сторонние и нечетно-сторонние; тогда мнимости возможны на первых и, на ряду с действительными координатами, невозможны на вторых. Но в настоящей заметке достаточно обсудить и более узкий вопрос о поверхностях одно- и дву-сторонних, как типичных представительницах своих классов.

 

 

 

[39]

Итак, пусть имеется поверхность S, данная в гауссовых уравнениях:

x = φ (u, v), y = χ (u, v), z = φ (u, v)    [24]

где u и υ суть криволинейные координаты на ней. Тогда кривая на этой поверхности выразится уравнением, связывающим координаты u и υ

σ (u, v) = 0    [25]

Согласно традиции, идущей от Гаусса, станем обозначать: частные производныя — соответственными буквенными индексами, поставленными при функциях, а вторые частные производныя—такими же двумя индексами, так что:

 

 

Далее, обозначаем функциональные детерминанты:

 

 

И, по Р, Гоппе:

 

 

где X, У, Z определены уравнениями [31].

Возьмем на поверхности S точку М (х, у, z), определяемую криво-линейными координатами (u, υ)). Тогда косинусы углов нормали к поверхности в этой точке М с осями координат будут:

 

 

[40]

 

дифференциал дуги кривой, выражаемой уравнением [25], будет:

 

 

Станем теперь, исходя из точки М, делать обход по поверхности, выражаемый уравнением [25] и, наконец, вернемся в ту же точку М, которую теперь, в качестве конечной, обозначим чрез  Ясно, что пространственные координаты ея  соответственно равны координатам x, у, z, так что

 

 

Но направление нормали к поверхности может оставаться прежним, так что

 

 

а может также измениться на обратное, так что

 

 

Первый случай соответствует поверхности двусторонней, второй же—односторонней. Оставляя в стороне первый, как не занимающий нас в настоящем параграфе, рассмотрим более внимательно второй. Итак, спросим себя, отчего же, формально-аналитически, произошло в этом втором случае такое обращение нормали. 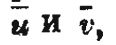Очевидно, от того, что, хотя пространственные координаты конца обхода  и тождественны с таковыми же начала его М, но криволинейные координаты  не тождественны с таковыми же u и v. Иначе говоря, хотя точка  есть одна и та же, что и M, точка в пространстве, но она—не одна и та же точка в отношении поверхности S. 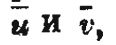Однако, при этом  таковы, что, в силу [34], должны быть совместными равенства:

 

[41]

 

 

Другими словами, функции x, у, z вполне инвариантны относительно подстановки вместо u и v величин РИС___

, но X, У, Z не инвариантны и, оставаясь неизменными по абсолютной величине, меняют знак свой.

Из равенств [37] может быть определена совершаемая при этом подстановка:

 

 

инвариантами которой являются функции [24]. Обозначая функциональный определитель

 

 

в силу инвариантности функций φ, χ, φ мы можем написать 

 

 

Чтобы знаки  были обратны знакам X, У, Z. необходима и достаточна перемена знака либо у всех трех числителей выражения [31], т. е. у А, B, C, либо у знаменателя Т. Но, как непрерывная, функция Т может изменить знак только проходя чрез O или чрез ∞, а для этого необходимо, чтобы А, В и C, все три зараз, прошли чрез O или чтобы прошла чрез ∞ хотя бы одна из этих величин, и при этом на произвольном пути между  и М, т. е, чтобы миновать это изменение при переходе от  к М было невозможно. Но это будет так—лишь при прохождении чрез особую линию на поверхности S. Быть так для любой точки М—не может. Поэтому, рассматривая более общий случай, оставим в стороне предположение о перемене знака

 

[42]

 

у T и обсудим перемену знаков у А, В и C. Но для изменения знаков у А, В и С, необходимо, как видно из формулы [40], чтобы получился таковой либо у А, В и С, либо чтобы знак детерминанта замещения  f  был отрицательный. Первое предположение требует перехода А, В и С либо чрез нуль, либо чрез бесконечность, а для этого опять необходимо, чтобы наш обход пересек особую линию поверхности S. Оставляя этот случай, как исключительный и уже исключенный, сущий вне рассмотрения, предполагаем следовательно отрицательный знак детерминанта замещения:

 

f <0    [41]

 

Простейшею линейною подстановкою переменных и и v будет подстановка вида:

 

 

Функциональный определитель этой подстановки есть:

 

 

Отрицательный знак он может иметь либо в зависимости от такового же у числителя, либо в зависимости от такового же у знаменателя.—В первом случае, т. е. когда постоянное число

 

 

мы имеем дело с такою поверхностью, у которой обращение по нормали происходит при обеих гауссовых координатах действительных или обеих—мнимых, ибо и в том и другом случае знаменатель определителя существенно положителен. Не трудно призвать в ней поверхность одностороннюю.

 

 

[43]

 

Если же, при наличии неравенства [44], имеет место еще неравенство

 

 

то, значит, одна из координат, либо u, либо υ, стала мнимой, вида

 

 

или

 

 

Тогда, следовательно, дело идет о поверхности двусторонней, ибо изменять знаки у косинусов углов нормалей не приходится.

Таким образом, переворот нормали определяется тем, остаемся ли мы на той же самой стороне (т. е. на поверхности односторонней), или переходим на другую сторону, одна координата которой действительная, а другая—мнимая (поверхность двусторонняя).

Во втором случае, т. е. когда постоянное число

 

 

а неравенство [46] сохраняет свою силу, переворота нормали нет, т. е. нет ни щ>и обеих действительных, ни при обеих мнимых координатах. Если же имеет место неравенство [45], то нормаль переворачивается при одной мнимой координате и не переворачивается при координатах обеих действительных или обеих мнимых.

Итак, при наличии определенного преобразования, знак числителя f в [43] будет определенным,—либо положительным, либо отрицательным. И вот, относительно этого самого, одного и того же, преобразо-

 

[44]

 

вания, поверхность односторонняя и поверхность двусторонняя ведут себя прямо противоположно. Если оно переворачивает нормаль у одной поверхности, то не переворачивает—у другой, и наоборот. В итоге, по отношению к данному преобразованию имеем:

 

 

 

Что касается до криволинейных отрезков, то этот вопрос решается рассмотрением элемента дуги ds. В выражении [33] для ds²/ p входят величины dx, dy, dz и dX, dY, dZ; после линейного преобразования [38] первые свой знак меняют во всяком случае, вторые же могут изменить его, или не изменить, причем это, раз преобразование установлено, зависит от рода поверхности. Соответственно изменению или неизменению знака, ds будет мнимым или действительным: когда ds окажется действительным на поверхности односторонней, то оно будет мнимым на поверхности двусторонней, и наоборот.—Этим кратким указанием ограничимся.

 

§ 9.  В качестве предварительного сообщения, к изложенному выше пусть присоединится еще несколько мыслей, по широте своего охвата и по ответственности

 

[45]

 

не притязающих, в этом кратком изложении, на полную обоснованность. Но ради закругленности теории мнимостей представляется полезным наметить ходы дальнейшей разработки и некоторые возможные применения. А кроме того, мне хотелось не оставить без отклика отпразднованный 14 сентября 1921 года, на пороге нового духовного синтеза, шестисотлетний юбилей кончины величайшего из выразителей целостного миропонимания. Думается, предложенное здесь истолкование мнимостей, в связи со специальным и с общим принципами относительности, по-новому освещает и обосновывает то Аристотеле-Птолемее-Дантово миропредставление, которое наиболее законченно выкристаллизовано в «Божественной Комедии».

Напомним, для начала, самый остов Дантовой космологии. Сделать это тем более необходимо, что в комментариях на «Божественную Комедию» обычно дается изображение: сфера Земли, окруженная сферами небесных светил, небом неподвижных звезд, кристалльным небом и, наконец, эмпиреем, причем Дантов путь, по выходе его из недр Земли, начерчен ломанной линией, спирально переходящей по концентрическим сферам и загибающейся на 180°, к зениту Сиона. Но этот чертеж не соответствует ни повествованию Данта, ни основам его космологии. Картина этой вселенной неизобразима эвклидовскими чертежами, как Дантовская метафизика несоизмерима с философией Канта. Математиками, — Хальстедом (1905), Вебером (1905), Симоном (1912), — уже отмечено предвосхищение Дантом неэвклидовой геометрии, например, в вопрошании явившегося Господа царем Соломоном, домогающимся узнать:

... можно ль треугольник начертить в полукруге, без «прямого» при процессе черчения?...

Итак, припомним путь Данта с Вергилием. Он начинается в Италии. Оба поэта спускаются по кручам воронкообразного Ада. Воронка завершается последним, наиболее узким кругом Владыки преисподней. При этом, обоими поэтами сохраняется во все

 

[46]

 

время нисхождения вертикальность — головою к месту схода, т.е. к Италии, и ногами — к центру Земли. Но, когда поэты достигают приблизительно поясницы Люцифера, оба они внезапно переворачиваются, обращаясь ногами к поверхности Земли, откуда они вошли в подземное царство, а головою — в обратную сторону (Ад, песнь XXIII):

⁷⁴По клочьям шерсти (Люцифера) и коре льдяной,

   Как с лестницы, спускалась тень Вергилья.

⁷⁶Когда же мы достигли точки той,

   Где толща чресл вращает бедр громаду, —

 Вождь опрокинулся туда главой

⁷⁹Где он стоял ногами, и по гаду

   За шерсть цепляясь, стал всходить в жерло:

   Я думал, вновь он возвращался к Аду.

⁸²«Держись, мой сын!» — сказал он, тяжело

   Переводя свой дух от утомленья:

   «Вот путь, которым мы покинем зло».

⁸⁵Тут в щель скалы пролез он, на каменья

   Меня ссадил у бездны и в виду

   Стал предо мною, полн благоговенья.

⁸⁸Я поднял взор и думал, что найду,

   Как прежде Диса; но увидел ноги,

   Стопами вверх поднятыми во льду.

⁹¹Как изумился я тогда в тревоге,

   Пусть судит чернь, которая не зрит,

  Какую грань я миновал в дороге.

⁹⁴«Встань на ноги», заговорил пиит ...

 

Миновав эту  грань (которой и до сих пор эвклидовская «чернь не зрит»), т.е. окончив путь и миновав центр мира, поэты оказываются под гемисферою противоположной той, «где распят был Христос»: они подымаются по жерлообразному ходу.

¹³³Мой вождь и я сей тайною тропою

    Спешили снова выйти в Божий свет

    И, не предавшись ни на миг покою,

¹³⁶Взбирались вверх — он первый, я во след,

     Пока узрел я в круглый выход бездны

    Лазурь небес и дивный блеск планет,

 ¹³⁹И вышли мы, да узрим своды звездны.

 

После этой грани поэт восходит на гору Чистилища и возносится через небесные сферы. — Теперь — вопрос: по какому направлению? Подземный ход, которым они поднялись, образовался падением Люцифера, низ-

 

[47]

 

вергнутого с неба головою. Следовательно, место, откуда он низвергнут, находится не вообще где-то на небе, в пространстве, окружающем Землю, а именно со стороны той гемисферы, куда попали поэты. Гора Чистилища и Сион, диаметрально противоположные между собою, возникли как последствия этого падения, и значит путь к небу направлен по линии падения Люцифера, но имеет обратный смысл. Таким образом, Дант все время движется по прямой и на небе стоит — обращенный ногами к месту своего спуска; взглянув же оттуда, из Эмпирея, на Славу Божию, в итоге оказывается он,  без особого возвращения назад, во Флоренции. Путешествие его было действительностью; но если бы кто стал отрицать последнее, то во всяком случае оно должно быть признано поэтическою действительностью, т.е. представимым и мыслимым, — значит, содержащим в себе данные для уяснения его геометрических предпосылок. Итак: двигаясь все время вперед по прямой и перевернувшись раз на пути, поэт приходит на прежнее место в том же положении, в каком он уходил с него. Следовательно, если бы он по дороге не перевернулся, то прибыл бы по прямой на место своего отправления уже вверх ногами. Значит, поверхность, по которой двигается Дант, такова, что прямая на ней, с одним перевертом направления, дает возврат к прежней точке в прямом положении; а прямолинейное движение без переворота — возвращает тело к прежней точке перевернутым. Очевидно, это — поверхность: 1°, как содержащая замкнутые прямые, есть  риманновская плоскость, и 2°, как переворачивающая при движении по ней перпендикуляр, есть поверхность односторонняя. Эти два обстоятельства достаточны для геометрического охарактеризования  Дантова пространства, как построенного по типу эллиптической геометрии. Напоминаем, что Риманн, пользуясь собственно дифференциальными методами исследования, не имел возможности рассмотреть форму полных поверхностей. В силу этого, предметом

 

[48]

 

его геометрических обсуждений были безразлично две, далеко не тождественные между собою, геометрии, из которых одна полагает в основу плоскость эллиптическую, другая же — сферическую. В 1871 г. Ф. Клейн указал, что сферическая плоскость обладает характером поверхности двусторонней, а эллиптическая — односторонней. Дантово пространство весьма похоже именно на пространство эллиптическое. Этим бросается неожиданный пучок света на средневековое представление о конечности мира. Но в принципе относительности эти общегеометрические соображения получили недавно неожиданное конкретное истолкование, и с точки зрения современной физики мировое пространство должно быть мыслимо именно как пространство эллиптическое, и признается конечным, равно как и время, — конечное, замкнутое в себе.

На этом поразительном юбилейном подарке Средневековью от враждебной ему галилеевской науки, дело однако не кончается. И вот некоторые дальнейшие сопоставления.

Вопрос идет о реабилитации Птолемее-Дантовой системы мира. Принцип относительности «доказывается» неудачею опыта Майкельсона и Морлея. Не сомневаясь в общем принципе относительности и лишь несколько недоумевая, что значит в специальном принципе «прямолинейное равномерное движение», коль скоро нет неподвижных координатных осей, я хотел бы, однако, задать простой вопрос о причине неудачи вышеупомянутого опыта. В основу опыта положена гипотеза о движении Земли, и когда последствий этого движения не обнаружилось, тогда стал придумываться ряд чрезвычайных новых гипотез, которыми хотели подпереть первую гипотезу о движении Земли. Но гипотеза, признанная наиболее основательной, — специальный принцип относительности, — будучи вполне приемлемой сама по себе, однако в корень уничтожает самую предпосылку Майкельсона, ибо утверждает, что никаким физическим опытом убедиться в предполагаемом движении

 

[49]

 

Земли невозможно. Иначе говоря, Эйнштейн объявляет систему Коперника чистой метафизикой, в самом порицательном смысле слова. А если так, то не проще ли было бы, чем хватать себя за ухо через голову, начать объяснение Майкельсоновской неудачи наиболее естественным предположением — о  ложности его основной предпосылки: предполагали, что опыт удастся, потому, что рассчитывали на скорость Земли (- гипотетическую! -) 30 км/сек; но опыт  не удался, и следовательно прежде всего нужно было заподозрить допущенную гипотезу и подумать, движется ли, в самом деле, Земля? — Земля покоится в пространстве — таково прямое следствие опыта Майкельсона. Косвенное следствие — это надстройка, именно утверждение, что понятие о движении — прямолинейном и равномерном — лишено какого-либо уловимого смысла. А раз так, то из-за чего же было ломать перья и гореть энтузиазмом якобы постигнутого устройства вселенной?

Но, кроме поступательного движения Земли, приходится иметь в виду еще вращательное, и тут, казалось, Коперник что-то «открыл». Этому предположению противостоит обобщенный принцип относительности, в формулировке  Ленарда гласящий: «при любых движениях, все явления природы должны протекать совершенно одинаково, будет ли наблюдатель или все окружающее пространство приведено в соответствующее движение». Иначе говоря, применительно к нашему частному случаю,  нет и принципиально не может быть доказательств вращения Земли, и в частности, ничего не доказывает пресловутый опыт Фуко: при неподвижной Земле и вращающемся вокруг нее, как одно твердое тело, небосводе, маятник так же менял бы относительно Земли плоскость своих качаний, как и при обычном, Коперниковском предположении о Земном вращении и неподвижности Неба. Вообще, в Птолемеевой системе мира, с ее хрустальным небом, «твердью небесною», все явления должны происходить

 

[50]

 

так же, как и в системе Коперника, но с преимуществом здравого смысла и верности земле, земному, подлинно достоверному опыту, с соответствием философскому разуму и, наконец, с удовлетворением геометрии. Но было бы большою ошибкой объявлять системы Коперниковскую и Птолемеевскую  равноправными способами понимания: они таковы — только в плоскости отвлеченно-механической, но, по совокупности данных, истинной оказывается последняя, а первая — ложной. Это прямое подтверждение великой поэмы, хотя и более чем через 600 лет.

Впрочем, и им углубленное понимание Птолемее-Дантовской системы только начинается, ибо современная научная мысль, совершенно неожиданно, подводит нас к Данте-Аристотелевской науке о началах сущего. Специальный принцип относительности выражается иногда в виде признаваемого ему равносильным  принципа предельности мировых скоростей: не может быть скоростей больших скорости света 3 • 10¹⁰ см/сек. Но, если это верно, то как же, по общему принципу относительности, может быть допущено движение небосвода вокруг Земли, для какового требуются скорости неизмеримо превосходящие вышеозначенный предел? Так, стравив оба принципа, противники второго, т.е. очевидно защитники коперниканства, думали опровергнуть источник возражений себе, но не вдумавшись достаточно, собственными руками вырыли себе яму.

Что собственно значит предельность величины 3 • 10¹⁰ см/сек ? Это значит вовсе не невозможность скоростей равных и больших с, а — лишь появление вместе с ними вполне новых, пока нами наглядно непредставимых, если угодно — трансцендентных нашему земному, кантовскому опыту, условий жизни; но это вовсе не значит, чтобы таковые условия были немыслимы, а может быть, с расширением области опыта, — и пред

 

[51]

 

ставимыми. Иначе говоря: при скоростях, равных с и тем более — больших с, мировая жизнь качественно отлична от того, что наблюдается при скоростях меньших с, и  переход между областями этого качественного различия мыслим только прерывный. Обращаясь к Птолемеевской системе, мы видим, что внутренняя ее область, с экваториальным радиусом

R=(23ч 3м 56,6с / 2π • 300000)км,

где 23ч 3м 56,6с есть продолжительность звездного времени по среднему солнечному времени, ограничивает собою все земное бытие. Это есть область  земных движений и земных явлений, тогда как на этом предельном расстоянии и за ним начинается мир качественно новый, область  небесных движений и небесных явлений, — попросту Небо. Этот демаркационный экватор, раздел Неба и Земли, не особенно далек от нас, и мир земного — достаточно уютен. А именно, в астрономических единицах длины радиус его R равен 27,522 средних расстояний Солнца от Земли. Итак, область небесных движений в 27,5 раз далее от Земли, чем Солнце; иначе говоря, граница ее — между орбитами Урана и Нептуна. Результат поразительный, потому что им Птолемее-Дантовское представление о мире подтверждается даже количественно, а граница мира приходится как раз там, где ее и признавали с глубочайшей древности. Граница мира была за Ураном, — о котором сведения были уже смутные. Но вдумаемся, что значит этот результат конкретно. — Характеристики тел движущейся системы, наблюдаемой из неподвижной, зависят от основной величины

β = √(1 - v²/c²),

где v есть скорость движения системы, а с - скорость света. Пока v менее с, β действительно, и все харак

 

 

[52]

 

теристики остаются имманентными земному опыту; при ν равном с, β=0, и при ν большем с, β делается мнимым. В двух последних случаях происходит двукратный качественный скачок соответственных характеристик. Так, в движущейся системе длина тел по направлению движения сокращается в отношении β:1, время — в отношении 1:β, масса — в отношении 1:β, и т.д.

Следовательно, на границе Земли и Неба длина всякого тела делается равной нулю, масса бесконечна, а время его, со стороны наблюдаемое — бесконечным. Иначе говоря, тело утрачивает свою протяженность, переходит в вечность и приобретает абсолютную устойчивость. Разве это не есть пересказ в физических терминах — признаков идеи, по Платону — бестельных, непротяженных, неизменяемых, вечных сущностей? Разве это не аристотелевские чистые формы? или, наконец, разве это не воинство небесное, — созерцаемое с Земли как звезды, но земным свойствам чуждое?

Так — на пределе, при β=0. Но за пределом, при ν>с время протекает в  обратном смысле, так что  следствие предшествует причине. Иначе говоря, здесь действующая причинность сменяется, — как и требует Аристотеле-Дантовская онтология, — причинностью конечною, телеологией, — и за границею предельных скоростей простирается царство целей. При этом  длина и масса тел делаются мнимыми. Когда для мнимостей  нет конкретного истолкования, такой результат кажется странным, и именно неконкретность мышления о мнимостях до сих пор заставляет избегать сделанные здесь выводы исследователей новой механики. Но пора повергнуть два пугала мысли — мнимость и непрерывность, пора избавиться от horror imaginarii и horror discontinuitatis!

Но, имея в виду предлагаемое здесь истолкование мнимостей, мы наглядно представляем себе, как, стянувшись до нуля, тело проваливается сквозь поверхность — носительницу соответственной координаты, и выворачивается через самого себя, — почему приобретает

 

[53]

 

 мнимые характеристики. Выражаясь образно, а при конкретном понимании пространства — и не образно, можно сказать, что пространство  ломается при скоростях, больших скорости света, подобно тому, как воздух ломается при движении тел, со скоростями, большими скорости звука; и тогда наступают качественно новые условия существования пространства, характеризуемые мнимыми параметрами. Но, как провал геометрической фигуры означает вовсе не уничтожение ее, а лишь ее переход на другую сторону поверхности и, следовательно, доступность существам, находящимся по ту сторону поверхности, так и мнимость параметров тела должна пониматься не как признак ирреальности его, но — лишь как свидетельство о его переходе в другую действительность. Область мнимостей реальна, постижима, а на языке Данта называется Эмпиреем. Все пространство мы можем представить себе  двойным, составленным из действительных и из совпадающих с ними мнимых гауссовых координатных поверхностей, но переход от поверхности действительной к поверхности мнимой возможен только через  разлом пространства и  выворачивание тела через самого себя. Пока, мы представляем себе средством к этому процессу только увеличение скоростей, может быть скоростей каких-то частиц тела, за предельную скорость с; но у нас нет доказательств невозможности каких-либо иных средств.

 

Так, разрывая время, «Божественная Комедия» неожиданно оказывается не позади, а впереди нам современной науки.

 

1922, VII, 3/17
Сергиев Посад

 

[54]

Основная часть настоящей работы (§§1—7) написана в бытность мою студентом, в августе 1902 года,  и тогда же сообщена проф. Л. К. Лахтину и некоторым, товарищам, помнится Н. Н. Лузину, ныне проф. 1-го Московского Университета. Весною 1921 года зги параграфы была пройдены заново, и к ним присоединен обобщающий § 6. 28 сентября ст. ст. (10 октября по ст. ст.) того ж 1921 года моя работа была доложена на чередном вторичном заседании Всероссийской Ассоциации Инженеров (ВАИ), в Москве. Летом 1922 года, в связя с появившейся возможностью напечатания работы, были добавлены § 9 и «Пояснение в обложке».

¹ В хронологической последовательности, сочинения, в которых раавивалась концепция комплексной плоскости, должны быть расположены таким порядком:

Н. Kühn (1690 — 1769), — Meditationes de quantitatibus imagi-nariie exhibentis. Мемуар этот напечатан автором в Novi Commentarii Асаdemiae Scientiàrum Imperialis Petropolitanac. T. 3, 1750.

Henri Dominique Truel в 1786 г. развил теорию изображения комплексных чисел и сообщил ее Августину Normand′y; напечатаны его сообщения были в 1810 году.

Caspar Wessel,—Ого Directionens analytiake Betegning. Доложено в 1797 году Датской Академии, напечатано в 1798 г. и вышло в свет в 1799 году; воспроизведено в Arch, for Math. ok. Nat. 18, 1896, а также во французском переводе под заглавием: Essai sur la représentation de la direction. Copenhagne, 1897.

Gauss применил изображение комплексных чисел посредством точек в своей диссертации Demonstratio nоvа etc. Helmstedt, 1793 (Werke, v, p. ö; немецкий перевод E. Netto в Ostwald"s Klassikern, N 14. Lpz, 1890. (См. также письмо Гаусса к Весселю от 18 декабря 1811 года). О простейших операциях над комплексами Гаусс печатно не говорит ранее 1825 года— Abhandlung uber Kartenprojectionen (Astronom. Abh. von Schumacher, Heft 3, Altona 1825; Werke 4, p. 189).

Еще: Gottingische gelehrten Anzeigen, Jahr 1881, St. 64, S. 625 и Theoria residuorum biquadraticorum, Commentatio 2-е, Höttingae, 1832, p. 16 art 38 et 39 (Werke, 2, p. 169).

[55]

J. Rob. Argand,—Essai sur une manière de représenter les quantités imaginaires dans les constructions geometriques. Paris, 1806. Есть издание 1873 года, сделанное R. Houel′eм.

Aббат Buée, — Sur quantités imaginaires («Philosophical Transactions», 1806).

Francais,—Nouveaux principes de Géométrie de position, et interpretation géométrique des symboles imaginaires («Annales des Mathématiques» T. 4, pp. 222, 228, 364. Т. 6, pp. 197, 1813 и 1816).

John Warren,—A Treatise on the Geometrical Representation of the Square Roots of Negative Quantities. Cambridge, 1828.—Дальнейшее развитие своей теории Уаррен дает в Philosophical Transactions, 1829, pp. 241—254, 339—359.

Mourey,—La vrai théorio des quantités négatives et des quantités prétedues imaginaires, Paris, 1828. Есть издание 1861 г.

O. Bellavitis.—Methodo delle equipollenze («Annali delle science del regno Lombardo-Veneto». T. 7, 1837).

Его же,—Sposizione del metodo delle equipollenze («Memorie della Società Italiana delle scienze». T, 25, Modena, 1854).—Eсть французский перевод: Exposition de la méthode des équipolences par G. Bellavitis, tradnit par Laisant. Paris, 1894.

A. Cauchy,—Sur les quantites géométriques (Cauchy,—Exercices d"Analyse et de Physique mathématique. T. 4, Paris, 1847, pp. 157—180).

Matzka,—Versuch einer richtigen Lehre von der Realität der Vorgebliche imaginären Grössen der Algebra. Прага, 1850.

H. Scheffler,—Ueber das Verhältnies der Arithmetik zur Geometrie, Braunschweig 1846.

Его же,—Der Situationskalkul, Braunschweig, 1851,

A. P. Möbius,—Abhaudlungen («Berichte der Königl. Sächs. Ges. d. Wiss», 1832—1858). связное изложение мыслей Мёбиуса см. в: Witzschel,—Grundlinien der neueren Geometrie, 1858.

F. Riecke,—Die Rechnung mit Richtungszahlen, Stuttgart, 1856.

Hoüel,—Sur la méthode d"analyse géométrique de M. Bellavitis. («Nouv. Ann. de Math.», 2-me série. T. 8, 1869),

Его же - Тhéorie élémentaire des quantités complexes par Hoüel Partie premiere, 1867.—Русский перевод в «Математическом Сборнике» Т. 5, Вып. I.

F. Gomes Texeira, professeur a l" Universite de Colmbre (Portugal). («Ann. de la Société scientifique de Bruxelle», 7-е аnnéе, 1883, pp, 417—427.—Приложено к «Mathesis» T. 3, 1883,—См. также заметку M. P. Mansion"a. Т. 3, pp. 13—16).

² Из числа других геометрических истолкований комплексных чисел следует упомянуть о приурочении их посредством стереографической проекции к сфере («Сфера Нейманна»), хорош известном из теории функций мнимого переменного.

 

[56]

 

Грегори (1813—1844) предложил особенное геометрическое представление дли мнимых количеств; а Максимилиан Марк дал еще интерпретацию, «с помощью которой он легко об"яснил периодичность не только интегралов простых, но и кратных». Но суть этих истолкований мне неизвестна, и я делаю упоминания о них, а равным образом и нижеследующие библиографическия указания, из вторых рук,

Gregory,—Оn the elementary principles of the application of algebraical symbols to Geometry («Cambridge Mathematical Journal». T. 2, 1841).—Дальнейшее развитие своей мысли Грегори предложил в сочиненна:

Gregory,—Exemples of the Differen. and Integral Calculus. Gambridge, 1841.

Maximllien Marie,—Theorie des fonctions variables imaginaires, Paris, 1874—1876. TT, 1—8.

³ W. R. Hamilton,—в Dublin Transactions, 17 (1837)), p. 393.

Его же,—Lectures on Quaternions, Dublin, 1853, введение. Подробное изложение этой теории см. в книге:

Otto Stolz  und J. A. Gmeiner, —Theoretische Arithmetic, 2-te Auflage. Lpz., 1902, X. Abechnitt, §§ 276 ff.

См. также: E. Study.—Theorie der Gemeinen und Höheren compleren Grössen (Encyklopadie der Mathematischen Wissenschаften, Lpz,1898—1904, I A 45 ¹/₀).

⁴ Формула Отокса (Stokes) гласит о тождестве двух интегралов, линейного и поверхностного.

 

 

Тут (φ, ϕ, θ суть три какие-либо, произвольные, конечные, непрерывные н одвозначиые функции точки в пространстве. S есть некоторая поверхность, ограниченная кривою s, dS и ds—их элементы, п—нормаль к элементу ds., Контур обходится по положительному направлению, т. е. такому, которое наблюдателю, стоящему на поверхности S, так, чтобы нормаль n шла от его ног к голове, представляется обратным направлению часовой стрелки (чертеж 13-й).

Одно на наиболее распространенных доказательств теоремы Стокса предложено Друде; оно излагалось о некоторыми вариациями неоднократно. См, напр.:

 

[57]

 

Paul Drude,—Physik des Aethers auf elektromagnetischer Grundlage, 2-te Auflage nеu bearbeitet von Walter König. Stuttgart, 1912, l/"¹⁰, §§ 20—25.

O. Д. Хвольсон,—Курс физики. Т. 1V1, СПБ., 1907. Ч. 2-я, гл. 1-ая, § 5, стр. 349—365.

Н. Шиллер,—Лекцяа по теории потенциальной функции, IV, § 25, стр. 201—206. («[Киевские] Университетские Известия» 1884 г.).

⁵ 0 делении певерхностей на одно-н дву-сторонние, кроме первоначальных заметок Листинга (Listing, Abhandlungen d. Königl. Gesells- chaft der Wissenschaflen zu Gottingen, Bd. 10) b Мёбиуса (Möbius, Gesammelte Werke. Bd.. 2, § 484) и не более двух параграфов у Darboux, — Lecons sur la théorie générale des surfaces, Part. 1, (n⁰ n⁰ 231, 232) имеются специальные работы:

N. Delaunay,—Lecons sur les surfaces n"ayant qu"un сoté. («Bulletin de la Société Mathématique de France». T. 26, 1898),

Л. К. Лахтин,—Заметка об односторонних поверхностях («Математический Сборник». Т, 24. Вып. 2, М., 1903, стр. 138—193).

Топологическая трактовка в:

М. Dehn und P. Heegaard,—Analysis Situs.

Encyklopädie der mathematischen Wissenschafften, III А В 2, SS. 153. ff).

Рассмотревие вопроса в порядке чисто-топологическом дано мною в курсе лекций по «Энциклопедии Математики».

Настоящее изложение примыкает к «Заметке»Л. К. Лахтина.

 

[60]

 

 

[61]

 

ПОЯСНЕНИЕ К ОБЛОЖКЕ.

 

Обложка настоящей книги резана но дереву Владимиром Андреевичем Фаворским. Как свойственно вообще этому художнику, так а здесь era гравюра ве просто украшает книгу, но входит конститутивно в ее духовный состав. Поэтому, данная работа Фаворского есть художество, насыщенное математическою мыслию. Опыт такого рода—может быть первый, в наше время возрождающейся гравюры. Кстати сказать, вот направление искусства, которому в общем синтетическом складе грядущей культуры предстоит еще богатая жатва. Не только не признательности художнику за чуткое сотрудничество, но и по существу культурных задач нашего времени, автору кнжгн казалось полезным дать несколько пояснений обсуждаемой обложки, в связи с кое-какими намеками на возможный смысл изложенной теория мнимостей, применительно к искусству.

 

Припомним несколько явлений психологии зрения. Если смотришь на пространство, через не слишком широкое отверстие, сам будучи в стороне от него, особенно при не слишком ярком освещении стены с отверстием, то в поле зрения попадает и плоскость стены; но глаз не может аккомодироваться одновременно н на видимом сквозь стену пространстве и на плоскости отварестия. Поэтому, сосредоточиваясь вниманием на освещенном пространстве, в отношении самого отверстия—глаз вместе и видит его и не видит. Он его видел, когда проникал чрев него вглубь пространства, а когда уже проникнул, то перестал ввдеть, но воспоминание о виденном не может оставить сознание: смутное, почти осязательного порядка, впечатление от этой стены безпрестанно будоражит в сознании тo, что было ранее видено. Сознание необходимо раздвояется между образом непосредственно зрительным н образом косвенно, посредственно - зрительным, даваемым чем-то вроде осязания. При этих условиях восприятия, в сознании наличны два элемента, или два слоя элементов,— однородных по своему содержанию, но существенно разнород-

 

[62]

 

ных no своему положению в сознании, ж в этом смысле не координируемых и взаимно исключающих друг друга.

Вид через оконное стекло еще убедительнее приводят к тому же раэдвоеняю: наряду с самым пейзажем, в сознании наличие ш стекло, ранее пейзажа наня увя денное, но далее уже не видимое, хоти я воспринимаемое осязательным зрением или даже просто осязанием, например, вогда мы касаемся его лбом. Отсюда — живописная я архитектурная проблема современного, т. е. затянутого стеклом, окна, как некоего лже-отверстяя н некоей лже-стены; в постройках с обширными стеклянными покрытиями, я даже стеклянными стенами, эта проблема сделалась весьма настойчивой.

Когда мы рассматриваем прозрачное тело, имеющее значительную толщину, например аквариум с водою, стеклянный сплошной куб (чернильницу) и прочее, то сознание чрезвычайно тревожно двоится между различными по положению в нем (сознания), но однородными по содержанию (—и в этом-то последнем обстоятельстве — источник тревоги—) воснриятнями обеих граней прозрачного тела. Тело качается в сознания между оценкой его, как нечто, т. е. тела, я—как ничто, зрительного ничто, поскольку оно прозрачно. Ничто зрению, оно есть нечто осязанию; но это нечто преобразовывается зрительным воспоминанием во что-то как бы зрительное. Прозрачное—призрачно.

 

Сквозящая зелень весенних рощ будит в сердце тревогу вовсе не только потому, что появляется «раннею весною», но я просто по оптической причине—своей прозрачности: давая стереоскопическую глубину пространства, своими точечными листочками, хотя бы и вовсе не «клейкими», эта зелень намечает глубинные точки пространства и, будучи густо распределенною, делает это с достаточной психологической принудительностью. От этого все пространство, овеществляясь, получает зрительно характер стекловидной толщи. Опять: оно есть и не есть, воистину—наглядно представленное Платоновское Τύ  μη ξν. И еще один пример, особенно внятный. Как-то мне пришлось стоять н Рождественской Сергиево-Посадской церкви, почтя прямо против закрытых царских врат. Сквозь резьбу их ясно виднелся престол, а самыя врата, в свой черед, были видимы мне сквозь резную медную решетку на анвоне. Три слоя пространства; но каждый из них мог быть видим ясно только особой аккомо- дицней зрения, я тогда два другие получали особое положение в сознания я, следовательно, сравнительно с тем, ясно видимым, оценивались как полу-существующие.

Итак, в зрительном представлении мира необходимо, наряду с образами собственно зримыми, различать образы отвлеченно-зрительные, присутствующие, однако, в представлении не-

 

[63]

 

устранимо, силою бокового зрения, осязания и прочих восприятий, не дающих чистой зрительности, но к ней приводящих, на нее намекающих. Иначе говоря, в зрительном представлена и есть образы зрительные, а есть—и как бы зрительные. Не трудно узнать в этой двойственности зрительно представляемого двойственную природу геометрической плоскости, причем собственно зрительные образы соответствуют действительной стороне плоскости, а отвлеченно-зрительные-мнимой. Ведь двусторонность геометрической плоскости н есть свмвол дву-разлнчного положения в сознании зрительных образов, но—взятая предельно, т. е. когда толща разделенных слоев пространства бесконечно маха, а несоединимость тех и других образов предельно велика. Если переднюю сторону плоскости мы видим, то о задней только отвлеченно знаем. Но отвлеченно знать о некотором наглядном образе, сущность которого—выенно и его наглядности, это значит иметь восприятие его каких-то иным, не зрительным, способом, но с коррективом на зрктельность чрез отвлеченное понятие или чрез образ воспоминания. Действительность, в зтох смысле, есть воплощение отвлеченного в наглядный материал, из которого и было получено отвлеченное; а мнимость—это воплощение того же самого отвлеченного, но н наглядном материале инородном. Если угодно, действительность есть адекватность абстрактного и конкретного (тавтегоричность), а мнимость—символичность (аллегоричность). В этом смысле я надлежит говорить о понятиях ощущений как ощущениях мнимых, или ощущениях мнимого-, это есть мнимость предельная. В самом деле, единственное содержание ощущения—это самая его чувственная наличность; мыслимое же ощущение—не просто ничто, но—другое ощущение (—ибо всякое понятие смывается с некоторым чувственным субстратом, точкою своего приложения—), апперцепируемое инородным понятием. Уместно вспомнить тут Мейнонговский термин Pseudoexietenz, хотя и вне намека на значение его у Мейнонга. Эти особливо установленные в сознании чувственные элементы и мнимые образы вполне соответствуют мнимым геометрическим образам поверхности. Наличие же мнимых восприятий во всяком конкретном опыте побуждает искусствоведение подумать о мнимом: теории изобразительных искусств надлежит, следовательно, как-то сказать свое слово о предлагаемом истолковании геометрических мнимостей.

 

Обратимся теперь в попытке Фаворского—воспользоваться различением двух родов зрительных образов, с тех чтобы художественно выразить теорию мнимостей.

Первая задача, предлежавшая граверу,—это было сохранить н утвердить целостность основной плоскости, потому что без целостной плоокости не было бы возможности не только изоб-

 

[64]

 

ражать на сторонах ея, но в различать самые стороны. Эта первая задача осуществлена надписями, удерживающими основную плоскость изображения на плоскости страницы, а также обозначена яда точек координатных осей буквами X, О, У и вертикалью, проходящею через X Самые буквы Х, О, У, достаточно массивные, служат той же целя. Устойчивость главной вертикали подкреплена еще приподнятостью, сравнительно с именем автора, приходящейся над вертикалью фамилии его.

 

Страница, как таковая—конечно, не белая, а бесцветная: она есть отвлеченная возможность изображений. В этой странице было бы ошибочно видеть бумажный лист, вещество, каковой сак по себе не есть ни плоскость, ни что-либо иное геометрическое; по под страницею надо разуметь безконечно-тонкое пространство изображений, как бы прозрачную пленку, наложенную на лист. Эта пленка, сама по себе, еще не есть та идя другая сторона изобразительной плоскости, а—вся плоскость, с обеими своими сторонами и всею своею толщею, хотя бы актуально бесконечно-малою. Эта плоскость художником создана.

 

Теперь художнику надо наглядно показать, как ту, так н другую сторону этого пленочного пространства в их качественной тональности. Передняя сторона плоскости, как непосредственно зримая, обладает теплотою чувственна воспринимаемого я выдвигается вперед, но никак не ближе к ьрителю, чем основная плоскость надписей. Большой прямоугольник, заштрихованный черным штрихом, по черноте штриха и по горизонтальности его, как теплых дает образ передней стороны плоскости. На прямоугольнике, выступая вперед, изображены, как чисто действительные образы, полу-зллннс я малый, сплошь черный прямоугольник — самые теплые и самые выступающие частя пленочного пространства. Тонкая белая каемка, показывая нх толщину, тем самым еще выдвигает нх, приближая к зрителю. Все это—собственно зрительные образы. Им противопоставляется правая от вертикали сторона чертгсжа, резанная почти исключительно белым штрихом. Это — мнимая сторона плоскости, оборот пленочного пространства, я притом не какого-либо его места, а той самой области, чтб под заштрихованным прямоугольником левой части. Главная линяя мнимой стороны есть дуга распрямляющейся гиперболы—мнимого придатка действительного эллипса, каковой придаток должно представлять себе касающимся эллипса у его вершине.

 

Чтобы прядать этой линия цветность, гравер сжал её серией горизонтальных белых штрихов,—яи на абстрактней бесцветности пленочного пространства появилась холодная белая линия: такого цвета, противоположного теплой черноте передней сто-

 

[65]

 

роны плоскости, эта, оборотная; белый цвет этого оборота удачно ноказан наверху справа, где помещена белая решетка.

 

Спрашивается, почему оборот бел? Ясное дело, что pat он должен быть неким остаточным следом от чуветвенно-воспрмня- того—черного, то ему, как дополнительному образу или остаточному следу, необходимо быть именно белым. Еще: зрительность, как субстрат действительных образов, выражена присутствием теплой черноты; следовательно, отсутствие зрительностн, т. е. некоторое иное восприятие, оформленное, как зрительное, необходимо представляется негативным— и зрительное, по форме, н незрнтельное, по содержанию. Выражать это призван белый штрих: он—как штрих, т. е. черный, но лишенный своей черноты, пустой внутри, штрих я не штрих сразу. Таких образом, эта правая часть представлена как бы не нарисованной, а выдавленной, выпуклой, данной не зрению, как таковому, а осязанию. Впечатление оборотности этой правой стороны усугубляется от начертанной зеркально ж тоже белым штрихом, в нижнем правом углу, буквы О. это—не какая-либо новая буква, а то же самое черно-штриховое О, что видно в нижнем левом углу, но воспринятое через плоскость. Можно пояснить соотношение правого и левого О так: представим себе, что на бумаге карандашей было бы написано О, которое выдавилось бы выпукло на обороте листа. Эта буква была бы, следовательно, я зрительной, и осязательной. Пусть, далее, этот лист установлен неподвижно. Если бы затем кому-нибудь было предложено изобразить рисунком этот лист, смотря на него спереди н осязая его оборах рукою, то получился бы рисунок, подобный обложке Фаворского, и с таким же размещением. Ведь, проследив ширину листа от О в X глазом, рисовальщик продолжил бы свое наблюдение— рукою, и именно с той точки, где отказался бы служить глаз, т. е. повел бы руку от точки X к О. Следовательно, точна плоскости постепенно удаляющиеся от вертикали, что через X, оказались бы на рисунке тоже удаляющимися от вертикали, но уже не влево, а вправо: движение рукн по диету сознавалось бы продолжением движения глаза. Поэтому, точка О, как осязательная, оказалась бы на изображении самой далекой от точки О, как зрительной; соотношение ах обеих было бы приприблизительно зеркальным, — приблизительно, потому что мера пространства осязательного не тождествена таковой же—зрительного.

 

То же должно сказать и обо всем чертеже, справа дающем зеркально - зрительную транспозицию осязательного строения оборотной стороны плоскости. Иначе говоря, приходится мыслить пленочное пространство изображения как бы расщепленным на

 

[66]

 

две стороны, с поворотом испода, плоскости, кан страницы книги, на 180° около вертикальной оси, проходящей через X.

 

Теперь-то и начинается решение главной трудности гравера—наглядно показать, что обе половины чертежа, правая н левая, не просто приложены друг к другу, хотя бы н разнокачественные, одна чисто-зрительная, другая зрительно-осязательная, но составляют именно две стороны одной плоскости. Граверу предстояло показать наглядно, что правая часть чертежа есть только познавательное, но не вещественное расщепление плоскости. Это достигнуто во-первых тем, что» я раз"еди- венные, эти стороны имеют каждая признак другой—в виде небольшого прорыва, к другой стороне, я этими двумя прорывами взаимная связь сторон вновь восстанавливается. Прорыв сквозь лицевую сторону плоскости произведен в санок выступающем ее месте, там где она наиболее убедительно действительна. Это сделано наглядно, какик-то ясновидческим переносом воспринимающего центра сознания—по ту сторону плоскости. Тогда там воспринимается этот же негативно-белый цвет оборота, с изображенным по нему выпуклым и зеркально обращенным символом мнимости i, подобным зеркальному О, оттуда это i было бы видимо начертанным прямо, но отсюда оно воспринимается зеркально: это—отсюда « видимое изображение там начертанного г, нля оттуда осязаемый выпуклый след здесь начертанного г. Изображенное белым штрихом, это i явно иного характера, нежели буквы X, О, У передней стороны плоскости, н Притом оно белее белого оборота плоскости, т. е. отвлеченнее. Этот прорыв лица есть вид, для зрительно-транспоцированный рельеф, оборота, того самого, что представлен правой половиной чертежа. Но этот прорыв не координирован с лицом плоскости и сразу—ближе черного прямоугольника я дальше его: нельзя координировать однородное, но противоположное по положению в сознания.

Обе стороны плоскости связываются я в правой частя чертежа,—обратным прорывом из мнимости в действительность. Но характер прорыва тут уж не наглядный, а отвлеченный, не четкое ясновидение, а расплывчатое воспоминание о покинутом зрительном пространстве, всплывающее на первых порах вступления в пространство осязательное. Такнм именно воспоминанием представлена часть уввого черно»штрихового эллипса по диагонально-заштриховавному черным же штрихом полю. Таков лоскуток действительной стороны, хотя я на границе мнимости; находясь среди мнимого пространства, он не координирован с ним. Этот лоскуток, в соединении с бело-штриховым восполнением эллипса по бело-штриховому же полю, передает флюктуацию геометрической фигуры при ея провале сквозь плоскость,

 

[67]

 

когда она не определилась еще, будучи и мнимой, и действительной сразу.

 

Возвращаемся к прорыву левой части чертежа. Резкий контраст полей, черного и белого, делает это i зрительным центром всей страницы, неудержимо сосредоточивающим на себе взгляд, вследствие чего все левая часть чертежа созерцается прямим зрением в потому стоит на странице и в ей плоскости крайне устойчиво. Но тогда правая часть изображения, особенно край ея, неизбежно видится очень смутно, зрением боковым, которое оттянуто левым прорывом. Вся прапая часть, и по характеру резьбы имеющая отвлеченный характер, окончательно теряет конкретность и устойчивость. Туманная плоскость правой части взображения, отделившись от плоскости страницы, колышется, вращаясь около основной вертикали, находит на зрителя, как бы захлопываемая на лицо книга, при неподвижности левой ел крышки. Это впечатление подвижности правой стороны чрезвычайно поддержано, во первых, трех-ступенчатостью ея плоскости (решевка, выше ея, т. е. ближе к зрителю,—горизонтальная штриховка, а еще выше—вторая решетка, в квадрате), во вторых — как бы перспективным схождением параллелей обеих решеток и горизонтальной штриховки внизу, слева, что опять наводит на мысль о наклонности всей правой части, как если бы лист обложки отогнулся по вертикали я стал бы сам собою открываться; в третьих—тому же композиционному и, вместе, функциональному вамыслу способствует некоторое расширение всей правой стороны гравюры» как бы в силу приближения правого ея края к глазу.

Наконец, остается сказать еще несколько слов о надписях. Мы начали с того, что ими устанавливается самая плоскость изображения. Но плоскость не могла бы быть устаиовлеиой нми, если бы они были только на ея передней стороне; тогда пространство страницы, обрезанное с лица, т. е. ограниченное  спереди, углублялось бы беспредельно внутрь страницы, и не могло бы быть речи об обороте плоскости. Следовательно, надписи должны установить не только переднюю границу плоскости, ея лицо, но и нижнюю, ея оборот, стянув собою все плоское пространство, как бы зажимая его между двумя стеклами. Надписям надлежит определить собою всю толщу плоскости. Фаворский достигает этого, приурочивая буквы или их элементы к равным сторонам плоскости, причем МН, например, помещено явно на передней стороне, что показано и горизонтальной штриховкой, присоединяющей пространства этих букв к левому прямоугольнику композиции; М, Т, И в слове „геометрии" отнесены к оборотной стороне, как начертанные белым штрихом, а И, Т, И в слове „мнимости"—флюктуируют, частью оставаясь

 

[68]

 

на лице, частью же проваливаясь на изнанку, как бы прошивая, простегивая собою толщу плоскости; последняя буква слова «мнимости» особенно выразительно несет ту же функцию.

Но обложка не вполне достигала бы своего назначения, еели бы надписи служили только целям графики, а самая графика их была бы чужда их смыслу. Очевидно, графические особенности надписаний должны не только держать плоскость, но и передать звуковое пространство интонаций голоса и выразить звуковую координацию слов. Примером того, как Фаворский решает эту задачу, служит хотя бы помещение фамилия автора выше имени, чем передается соответственное интонационное подчеркивание; далее, в слове «мнимости» подчеркнутой оказывается первая его часть ударяемая, имеющее же смысл пояснительный и произносимое вполголоса «в геометрии»—попадает на обложке в мнимую, т. е. полу-видимую часть плоскости и т. д.

 

Таково в основных чертах толкование геометрической композиции Фаворского.

 

1922. VII. 29 (VIII 11).

 

Ипользован: http://www.bookshunt.ru/b5083